Statistical Field Theory

Statistical field theory provides a universal description of many-body systems in the vicinity of a critical point.The strength of correlations increases for decreasing spatial dimensions. Our group is mainly interested in systems with one-dimensional spatial extension, for which there are highly efficient methods to treat strongly correlated dynamics. Many models are integrable so they can be treated using exact analytic methods using conformal field theory, S-matrix and form factor bootstrap, and Bethe Ansatz methods. An even larger class of these systems can be treated considering them as perturbations of integrable models, or using e.g. semiclassical approximation. In addition, powerful numerical tools such as different versions of the truncated Hamiltonian approach, and matrix product state based approaches can also be applied.

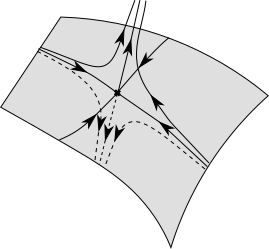
Exactly solvable models 

In one spatial dimensions, a lot of quantum many-body systems are exactly solvable. Such models include certain spin chains and Bose gases, which describe real physical systems such as e.g. one-dimensional magnetic materials, and ultracold atoms captured in an elongated trap. Some of these systems can be described with free fermions, however, in most cases they are interacting and strongly correlated, making them an interesting playground both for theoretical and experimental physics. Integrable many-body models are usually solved by means of the Bethe Ansatz, which can construct the exact spectrum, and correlation functions both in their ground states and in thermodynamic settings including finite temperature and/or density of excitations. These systems host a number of exotic phases and excitations, and near the vicinity of critical points they are related to conformal field theories and other integrable models of quantum field theory.

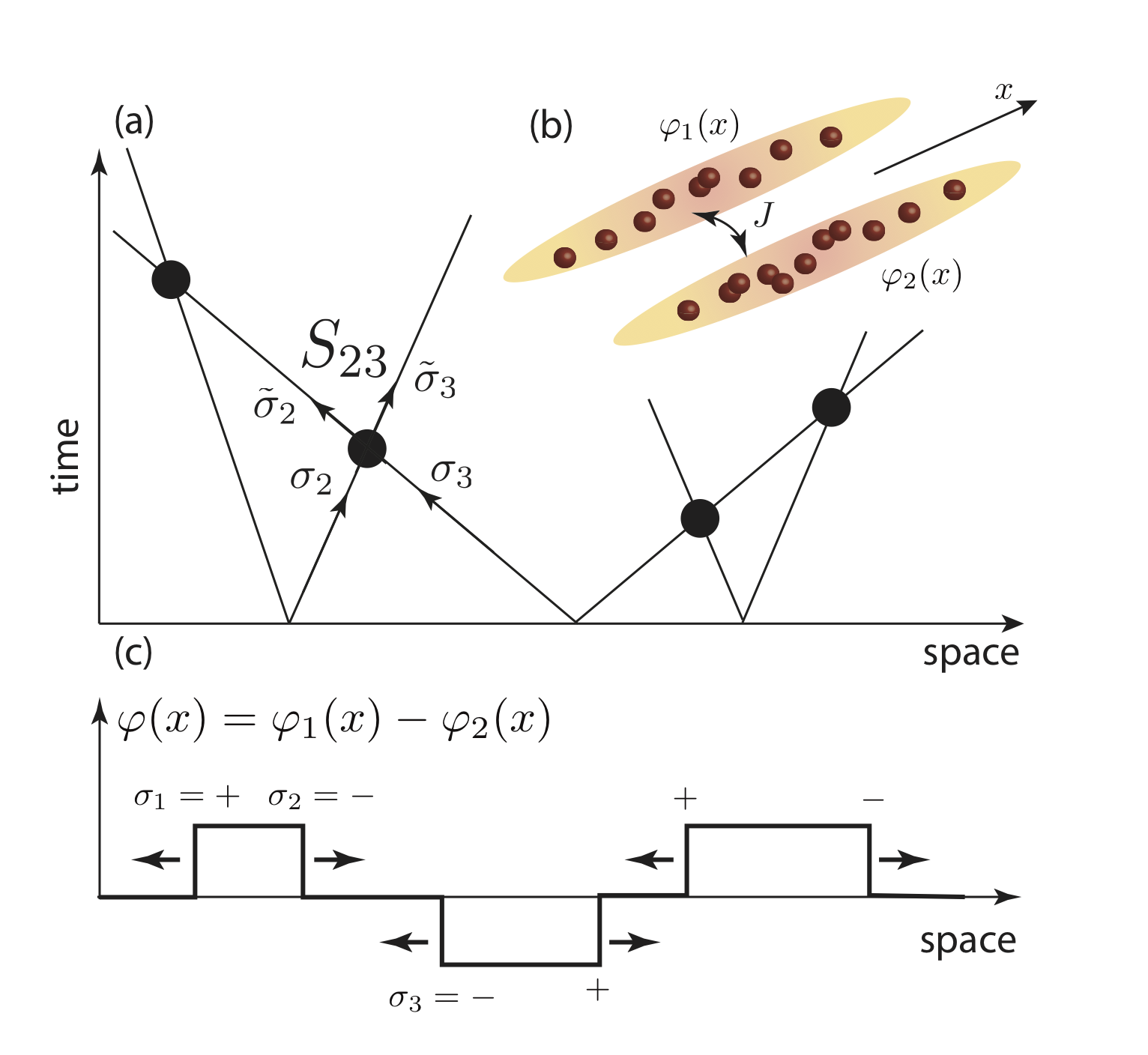Non-equilibrium dynamics

Due to recent developments in experimental techniques, non-equilibrium behaviour of quantum many-body systems is at the forefront of contemporary research. A paradigmatic and also experimentally realistic protocol is a quantum quench, when a system is suddenly brought out of equilibrium either by an abrupt change of a parameter in the Hamiltonian, or by connecting two subsystems which are in different equilibrium systems. In the latter case time evolution may lead to the formation of a non-equlibrium steady state. 

Integrability and its breaking has a profound effect on the non-equlibrium dynamics. In recent years, many new theoretical ideas have been developed, such as eigenstate thermalisation hypothesis, generalised Gibbs ensemble, prethermalisation, non-equilibrium steady states, generalised hydrodynamics.  Many universal features of non-equlibrium quantum dynamics have been discovered, e.g. the light-cone spreading of correlations and related generation of entanglement, along with some surprising effects of interactions on the time evolution.